BETWEEN THE LINES: JOAQUÍN TORRES-GARCÍA’S CONSTRUCTIVE COMPOSITION
 |
 |
Joaquín Torres-García (1874-1949) was born in Montevideo, Uruguay, but spent most of his adult life in Europe working with such major figures of modern art as Piet Mondrian, Theo van Doesburg, Juan Gris, and Pablo Picasso. In 1934 he returned to Uruguay, where he began a new phase of his career dedicated to teaching (at his workshop, the Taller Torres-García) and cultivating his theory of Constructive Universalism. A transatlantic figure, he catalyzed the development of abstract art in South America, drawing connections between pre-Columbian art and European modernism.
A foundational work in the collection of the Art Museum of the Americas, Constructive Composition (1943) exemplifies the ways in which the twentieth-century Uruguayan artist Joaquín Torres-García sought to create images of universal order. This painting, made of primary colors and a grid with easily recognizable pictographs exemplifies his ideas about harmony and universalism. You can watch a short video about this painting and its fascinating artist on the Constellations website.
Although he frequently explored the pure, geometric abstraction of forms and colors, Torres-García did not exclude figuration, or the presence of recognizable objects, from his works. In Constructive Composition, for example, he integrated pictographs (symbols that represent an image or idea, such as a heart or boat) within a constructivist grid. Torres-García believed that this relationship between the geometric structure of the painting and its symbolic content embodied an ideal harmony within the universe. He called this theory Constructive Universalism. In some of his paintings, he used the special properties of the golden ratio (see sidebar) to achieve an even greater feeling of integration with nature and the cosmos. To more perfectly express these universal relationships, Torres-García limited his palette to the most basic and pure colors – red, yellow, and blue (the primary colors), and white and black.
A philosophy of art developed by Torres-García in the 1930s, Constructive Universalism sought to combine the “reason” of geometry (Constructivism) with the spiritual “intuition” of man and nature (Universalism). The term “Constructivism” refers to a European tradition of abstract art based on geometric elements – lines, squares, planes – and characterized by simplicity and precision. Torres-García evoked the “universal” to describe organic sources of abstract art found in ancient (American) civilizations. In its integration of the constructivist grid and universal pictographs, Constructive Universalism aimed to restore balance and harmony to the (pictorial) world.
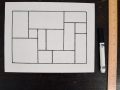
To make your own Constructive Composition, begin by thinking about the kinds of objects and symbols that are most meaningful in your life. Do you play a sport? Do you love animals or enjoying spending time in nature? Maybe you excel at math. Design pictographs that represent your personality or reflect some of your own experiences – moving to a new home, exploring your hometown, traveling the country or the world, starting school. The instructions below explain how to make a golden rectangle using a ruler, but you can experiment with squares and rectangles of different (non-“golden”) proportions.
You will need:
- A ruler
- Paper
- Watercolor paints, crayons, colored pencils, or markers
- A black marker
- A compass and a piece of cardboard larger than your paper (optional for making a golden rectangle)
Step 1. Make the grid.
The Greek mathematician Euclid first defined the golden ratio around 300 BCE. Found in nature and used by artists and architects for millennia, the golden ratio is thought to have special mystical properties related to the ideas of universal order, structure, and harmony. Torres-García is known to have used the golden ratio in his constructivist paintings.
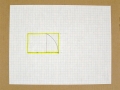
Note: To make a golden rectangle, follow Steps 1a-1e. The rectangle in the upper left corner of the example is a golden rectangle.
Begin by using the ruler to draw a variety of rectangles and squares in a pattern. (Alternatively, simply draw rectangles and squares without a ruler; this will result in a more informal composition.) In the example, all of the rectangles were traced with a pencil first and then re-drawn with a black marker.
Step 1a. To make a golden rectangle, first draw a square. Recommendation: Practice making a golden rectangle on graph paper first.
Step 1b. Extend two parallel lines from the top and bottom sides of the square.
Step 1c. Mark the midpoint of the bottom side of the square.
Step 1d. Position the point of the compass on the midpoint and extend the pencil to the upper right corner of the square. Draw an arc from the upper right corner of the square to the lower parallel line. Recommendation: place a piece of cardboard underneath the paper to anchor the compass in place.
Step 1e. With the ruler, draw a perpendicular line from the point at which the arc meets the lower parallel line to the upper parallel line. This is a golden rectangle.
Step 2. Choose colors. Use colored pencils, markers, or crayons to add color to some or all of the rectangles. If using watercolors, be sure to let the painting dry before moving on to Step 3.
Step 3. Add pictographs to the grid with the black marker. Personalize the composition with as many symbols as you like or none at all (Torres-García sometimes created constructivist compositions without any pictographs at all). Be creative and have fun!
What does your painting say about you? Next time, create a composition for someone else using symbols and pictographs that remind you of him or her.
The Math of the Golden Ratio
Any line can be divided into the golden section in which the ratio of the long section (A) to the short section (B) is equal to the ratio of the entire line (A+B) to the long section so that AB = A+BA. The numerical value of the golden ratio, AB, is determined through the quadratic formula, and is approximately 1.618, commonly denoted by phi (Φ), or the golden number. A golden rectangle is a rectangle in which the ratio of the long end to the short end is equal to Φ. The numerical value of Φ is determined using the quadratic equation: ax² + bx + c = 0. Solving for x results in this equation: x = -b±√b²-4ac2a. Plugging in the ratio AB gives AB = x = 1+√52, which is then denoted by Φ. Finally, Φ = 1+√52 ≈ 1+2.236067977499789…2 ≈ 3.236067977499789…2 ≈ 1.61803.
External links:
- The Golden Ratio – This website contains additional information about the golden ratio.
- Taller Torres-García – This website, maintained by the artist’s daughter-in-law, will include a catalogue raisonné beginning in 2014. Cecilia de Torres is an authority on Torres-García and many of the artists who studied at the Taller.
Lesson plan by Caroline J. Dubinsky. Photo credits: Art Museum of the Americas, Caroline J. Dubinsky.